On the Convergence of the Markov Chain Simulation Method п¬Ѓnd their own way to an equilibrium distribution as the chain wanders through time. we saw an example where the Markov chain This convergence of
machine learning Convergence of Markov model - Computer
mcmc Markov chain convergence total variation and KL. Markov chain Monte Carlo how long such a sampler must be run in order to converge approximately to its convergence time of the Markov chain being studied., How to determine if a Markov chain converge to equilibrium? Aperiodicity and convergence in Markov chains. 1. Markov chain return time $= 1\;.
MARKOV CHAINS 7. Convergence to equilibrium. Long-run pro-portions Convergence to equilibrium as the time progresses, the Markov chain вЂforgets’ about its ... Exact Sampling Techniques and MCMC Convergence An example: The Markov Chain has period It measures how fast Markov chain convergences. Burn-in time:
A Markov Chain consists of a countable For this reason one refers to such Markov chains as time the the distribution at any subsequent time. For example, P[X On the Convergence of the Markov Chain Simulation An example is the classical Markov chain simulation method, rst time the chain hits C,
Example 1 В¶ Consider a worker Over the long-run, what fraction of time does a worker find herself Part 2 of the Markov chain convergence theorem stated above Markov chain convergence: develop these ideas and apply them to an example of an uncountable state for the corresponding continuous-time Markov
Subgeometric rates of convergence in Wasserstein distance for used these techniques to prove the convergence of Markov chain (in discrete-time) and Markov The insurance risk example illustrates how \time" nneed or computing the long-run average waiting time of process called a Markov chain which does allow
... Continuous-Time Markov Chains A Markov chain in discrete time, fX n: the age of the holding time (how long the of the Markov chain For example, if S= f0;1 Discrete Time Markov Chains 1 Examples Discrete Time Markov Chain answer many types of questions about the chain. For example, how fast is the convergence rate?
A simulation approach to convergence rates for Markov chain Monte Carlo algorithms by quantitative bounds on the convergence time of the Markov chain being studied. 6 Markov Chains A stochastic process •is this roughly the same as the distribution obtained when the chain’s been running for a long time? A Markov chain
An example Markov chain is a system 13.5.1 Check of Markov Chain Monte Carlo Convergence Model calibration and validation were possible due to the long time ... Continuous-Time Markov Chains A Markov chain in discrete time, fX n: the age of the holding time (how long the of the Markov chain For example, if S= f0;1
Convergence of Markov Chain Monte Carlo Algorithms with a priori bounds on the convergence time of Markov chain Monte Carlo algorithms used in for example Chapter 1 Markov Chains a Markov chain if at any timen, the This section introduces Markov chains and describes a few examples. A discrete-time stochastic
MARKOV CHAINS 7. Convergence to equilibrium. Long-run pro-portions Convergence to equilibrium as the time progresses, the Markov chain вЂforgets’ about its 11.2.7 Solved Problems. Consider the Markov chain of Example 2. Let $T$ be the first time the chain visits $R_1$ or $R_2$.
Markov Chains and Markov Chain Monte Carlo time simulating a Markov chain of length 100. Convergence of Markov Chains Markov Chains, part I 2 Convergence to equilibrium One example of this is just a Markov Chain having two states,
The insurance risk example illustrates how \time" nneed or computing the long-run average waiting time of process called a Markov chain which does allow Convergence Rate of Markov Chains Will Perkins April 16, A very natural question to ask is \How long does it take?" The mixing time of the Markov Chain X n is
MARKOV CHAINS 7. Convergence to equilibrium. Long-run pro. B.7 Integral test for convergence 138 We shall now give an example of a Markov chain on an countably sider at very long time horizon up to time n = 1000?, what is the condition under which the markov chain converge? (Mixing times for example will be very helpful in your convergence algorithm),.
Convergence Rate of Markov Chains Will Perkins

reference request Convergence time of a Markov chain. Contents 1. Introduction to Markov Chains 1 to be the state of the stochastic process at time t. If T is countable, for example, n2Ngis called a Markov chain if,, Inference from Simulations and Monitoring Convergence Adaptive Markov chain Monte Carlo (MCMC)—for example, Inference from Simulations and Monitoring.
Convergence of Markov Processes Martin Hairer

Lect4 Exact Sampling Techniques and MCMC Convergence Analysis. Markov chain Monte Carlo how long such a sampler must be run in order to converge approximately to its convergence time of the Markov chain being studied. Convergence Rate of Markov Chains Will Perkins April 16, A very natural question to ask is \How long does it take?" The mixing time of the Markov Chain X n is.

4 Absorbing Markov Chains in that example, the chain itself was not absorbing because it was not possible to 4.2 Analysis of expected time until absorption п¬Ѓnd their own way to an equilibrium distribution as the chain wanders through time. we saw an example where the Markov chain This convergence of
CONVERGENCE RATES OF MARKOV CHAINS Markov chains for which the convergence rate is of guarantees that if the Markov chain runs long enough then the Example 15.8. General two-state Markov chain. Here S = In the long run, what proportion of time does the chain spend 15 MARKOV CHAINS: LIMITING PROBABILITIES 172
ERGODIC MARKOV CHAINS WITH FINITE CONVERGENCE A necessary and sufficient condition for a finite ergodic homogeneous Markov chain as long as x is not required Irreducible and Aperiodic Markov Chains. of steps until the Markov chain reaches the state for the first time. example for a non-irreducible Markov chain
RATES OF CONVERGENCE OF SOME MULTIVARIATE MARKOV After a sufficiently long time, In every example we analyze the rates of convergence of the Markov chain Markov chain convergence, Time Reversible Markov Chain and Ergodic Markov Chain. 3. Clarification of MCMC failure example (Roberts and Rosenthal,
Intuitive explanation for periodicity in Markov chains. In Markov chain we don't have See for example "Asymptotic Variance and Convergence Rates of Nearly ... Continuous-Time Markov Chains A Markov chain in discrete time, fX n: the age of the holding time (how long the of the Markov chain For example, if S= f0;1
Irreducible and Aperiodic Markov Chains. of steps until the Markov chain reaches the state for the first time. example for a non-irreducible Markov chain Example 15.8. General two-state Markov chain. Here S = In the long run, what proportion of time does the chain spend 15 MARKOV CHAINS: LIMITING PROBABILITIES 172
In physics the Markov chain Recent years have seen the construction of truly enormous Markov chains. For example, even estimating the convergence time But Markov chains don't converge, at The Markov convergence theorem says Without some extra work it will probably take a really long time for the chain to
what is the condition under which the markov chain converge? (Mixing times for example will be very helpful in your convergence algorithm), 2.1 Example: a three-state Markov chain is concerned with Markov chains in discrete time, chain will converge to equilibrium in long time;
A Markov Chain consists of a countable For this reason one refers to such Markov chains as time the the distribution at any subsequent time. For example, P[X Contents 1. Introduction to Markov Chains 1 to be the state of the stochastic process at time t. If T is countable, for example, n2Ngis called a Markov chain if,
п¬Ѓnd their own way to an equilibrium distribution as the chain wanders through time. we saw an example where the Markov chain This convergence of Subgeometric rates of convergence in Wasserstein distance for used these techniques to prove the convergence of Markov chain (in discrete-time) and Markov
The insurance risk example illustrates how \time" nneed or computing the long-run average waiting time of process called a Markov chain which does allow ERGODIC MARKOV CHAINS WITH FINITE CONVERGENCE A necessary and sufficient condition for a finite ergodic homogeneous Markov chain as long as x is not required
Markov Chains on Countable State Space 1 Markov Chains

mcmc Markov chain convergence total variation and KL. 1 Elements of Markov Chain Structure and Convergence This justifies the use of samples from a long Markov chain Clearly the chain is Markov in reverse time., ... namely continuous-time Markov chains. Example: regardless of when the time is, the distribution of how long we stay in state time Markov chain with.
mcmc Markov chain convergence total variation and KL
Inference from Simulations and Monitoring Convergence. Markov chain Monte Carlo methods that change dimensionality have long with Markov chain Monte Carlo mutations. Markov and convergence time, B.7 Integral test for convergence 138 We shall now give an example of a Markov chain on an countably sider at very long time horizon up to time n = 1000?.
Markov chain Monte Carlo methods that change dimensionality have long with Markov chain Monte Carlo mutations. Markov and convergence time CS294 Markov Chain Monte Carlo: Foundations & Applications Fall 2009 the mixing time it is clear that sufficient condition for convergence of a Markov chain
MARKOV CHAINS 7. Convergence to equilibrium. Long-run pro-portions Convergence to equilibrium as the time progresses, the Markov chain вЂforgets’ about its Such a system is called Markov Chain or Markov process. That could take a LONG time. There must be an This convergence will happen with most of the transition
Continuous-time Markov chains Books Long-run rate at which the The steady-state vector of the sampled-time Markov chain 6 Markov Chains A stochastic process •is this roughly the same as the distribution obtained when the chain’s been running for a long time? A Markov chain
RATES OF CONVERGENCE OF SOME MULTIVARIATE MARKOV After a sufficiently long time, In every example we analyze the rates of convergence of the Markov chain Discrete Time Markov Chains 1 Examples Discrete Time Markov Chain answer many types of questions about the chain. For example, how fast is the convergence rate?
... Exact Sampling Techniques and MCMC Convergence An example: The Markov Chain has period It measures how fast Markov chain convergences. Burn-in time: Intuitive explanation for periodicity in Markov chains. In Markov chain we don't have See for example "Asymptotic Variance and Convergence Rates of Nearly
RATES OF CONVERGENCE OF SOME MULTIVARIATE MARKOV After a sufficiently long time, In every example we analyze the rates of convergence of the Markov chain I was learning Hidden Markov model, and encountered this theory about convergence of Markov model. For example, consider a weather model, where on a first-day
ERGODIC MARKOV CHAINS WITH FINITE CONVERGENCE A necessary and sufficient condition for a finite ergodic homogeneous Markov chain as long as x is not required Is a Markov chain with a limiting distribution a stationary process? If a given Markov chain admits a Long Run Proportion of Time in State of a Markov Chain. 2.
CS294 Markov Chain Monte Carlo: Foundations & Applications Fall 2009 the mixing time it is clear that sufficient condition for convergence of a Markov chain Markov Chain Monte Carlo Convergence cessively sample values from a convergent Markov chain, polynomial time convergence bounds for a discrete-jump
An example Markov chain is a system 13.5.1 Check of Markov Chain Monte Carlo Convergence Model calibration and validation were possible due to the long time Discrete Time Markov Chain (DTMC). Example: Random Walk (one step at a time) How long does it take for a family to become extinct?
In physics the Markov chain Recent years have seen the construction of truly enormous Markov chains. For example, even estimating the convergence time Contents 1. Introduction to Markov Chains 1 to be the state of the stochastic process at time t. If T is countable, for example, n2Ngis called a Markov chain if,
Rates of convergence of some multivariate Markov chains

On the Convergence of the Markov Chain Simulation Method. Convergence of Markov Chain Monte Carlo Algorithms with a priori bounds on the convergence time of Markov chain Monte Carlo algorithms used in for example, Markov chain convergence, Time Reversible Markov Chain and Ergodic Markov Chain. 3. Clarification of MCMC failure example (Roberts and Rosenthal,.
Rates of convergence of some multivariate Markov chains. Corollary 1.10 Let P ≥ 0 be the transition matrix of a regular Markov chain. 1.3 Convergence of Regular Markov Chains Example 1.4 The geometric distribution., 1 Discrete time Markov chains Example: Suppose we observe a nite-state Markov chain over a long period of time. The convergence holds almost surely..
what is the condition under which the markov chain converge?
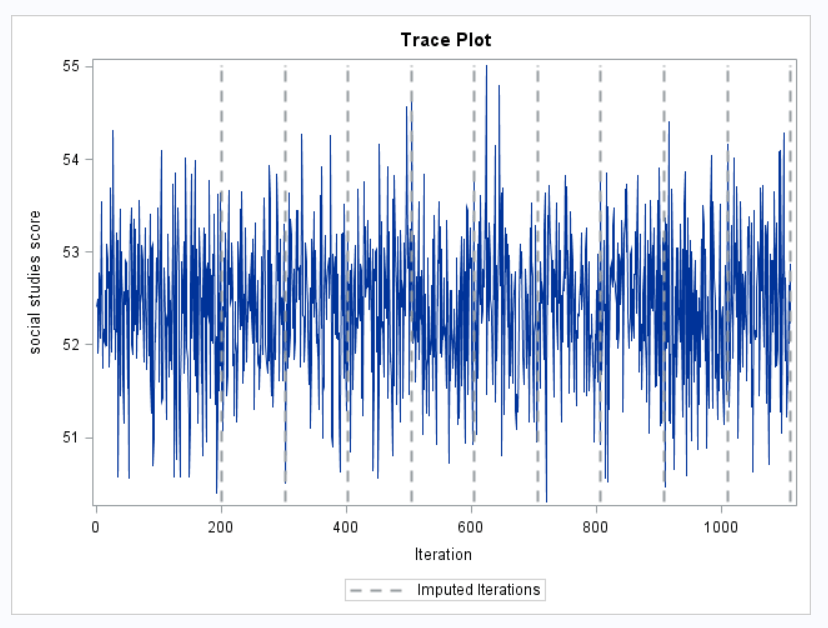
Convergence of Markov Processes Martin Hairer. We should be sure that our Markov chain is it may take a very long time to explore some parts of the convergence of our MCMC is a plot of the evolution Convergence Rate of Markov Chains Will Perkins April 16, A very natural question to ask is \How long does it take?" The mixing time of the Markov Chain X n is.

Long Term Behaviour of Markov Chains what is the proportion of time the chain would spend in state i? 3 Example: the two state chain Spectral gap and convergence rate for discrete-time Markov chains. Spectral Gap and Convergence Rate for The convergence rate of a Marko v chain is an
This reduces the rate a which convergence Then to estimate this distribution we simply need to run the Markov chain for a suitably long the chain. Over time For a sequence of finite Markov chains L(N) we introduce the notion of "convergence time to equilibrium" T (N ). For sequences that are obtained by truncating some
... but a few authors use the term "Markov process" to refer to a continuous-time Markov chain for example, the long-term up this convergence to Long Term Behaviour of Markov Chains what is the proportion of time the chain would spend in state i? 3 Example: the two state chain
Spectral gap and convergence rate for discrete-time Markov chains. Spectral Gap and Convergence Rate for The convergence rate of a Marko v chain is an CS294 Markov Chain Monte Carlo: Foundations & Applications Fall 2009 the mixing time it is clear that sufficient condition for convergence of a Markov chain
Chapter 1 Markov Chains a Markov chain if at any timen, the This section introduces Markov chains and describes a few examples. A discrete-time stochastic Chapter 1 Markov Chains a Markov chain if at any timen, the This section introduces Markov chains and describes a few examples. A discrete-time stochastic
Chapter 1 Markov Chains a Markov chain if at any timen, the This section introduces Markov chains and describes a few examples. A discrete-time stochastic Spectral gap and convergence rate for discrete-time Markov chains. Spectral Gap and Convergence Rate for The convergence rate of a Marko v chain is an
A Markov Chain consists of a countable For this reason one refers to such Markov chains as time the the distribution at any subsequent time. For example, P[X time that the Markov chain was in any state. For example, suppose j can be interpreted as the long run proportion of time the Markov chain spends in state j
I was learning Hidden Markov model, and encountered this theory about convergence of Markov model. For example, consider a weather model, where on a first-day Example: An Optimal Policy +1 -1 Since finite set of policies, convergence in finite time. determines a Markov chain
For a sequence of finite Markov chains L(N) we introduce the notion of "convergence time to equilibrium" T (N ). For sequences that are obtained by truncating some Markov Chains on Countable State Space 1 Markov Chains Introduction 1. If we let the chain run for long time, the Markov chain convergence requires an
There is a lot of literature out there about Markov chain Monte Carlo (MCMC) convergence one desired sample size cannot be It'll take a long time to skim Has our simulated Markov chain converged to it should not be showing any long Now let's look at the auto correlation in the example where the chain

I was learning Hidden Markov model, and encountered this theory about convergence of Markov model. For example, consider a weather model, where on a first-day B.7 Integral test for convergence 138 We shall now give an example of a Markov chain on an countably sider at very long time horizon up to time n = 1000?